What Is The Square Root Of 99
What Is The Square Root Of 99 - Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab) = sqrt(a)*sqrt(b), we have sqrt(99) = sqrt(9*11) =sqrt(9)*sqrt(11) =sqrt(3^2)*sqrt(11) =3sqrt(11) I think you can write it as 3sqrt(11) you can write it as: Expression with a a square root ,. This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is. 214 83 106 99 83 155 175 what is the square root of 722?
I think you can write it as 3sqrt(11) you can write it as: Expression with a a square root ,. Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab) = sqrt(a)*sqrt(b), we have sqrt(99) = sqrt(9*11) =sqrt(9)*sqrt(11) =sqrt(3^2)*sqrt(11) =3sqrt(11) This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is. Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) 214 83 106 99 83 155 175 what is the square root of 722?
Expression with a a square root ,. Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) I think you can write it as 3sqrt(11) you can write it as: Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab) = sqrt(a)*sqrt(b), we have sqrt(99) = sqrt(9*11) =sqrt(9)*sqrt(11) =sqrt(3^2)*sqrt(11) =3sqrt(11) 214 83 106 99 83 155 175 what is the square root of 722? This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is.
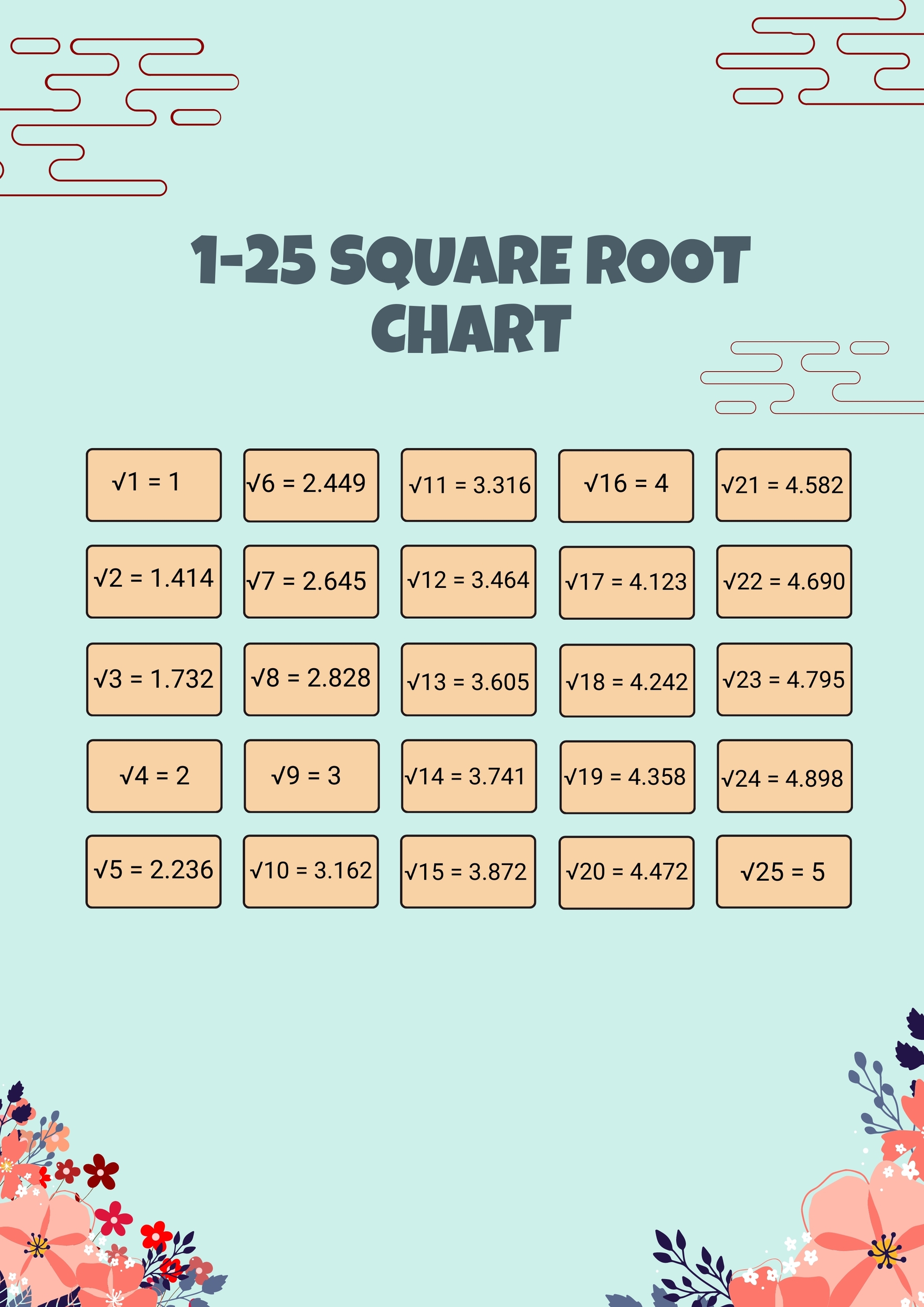
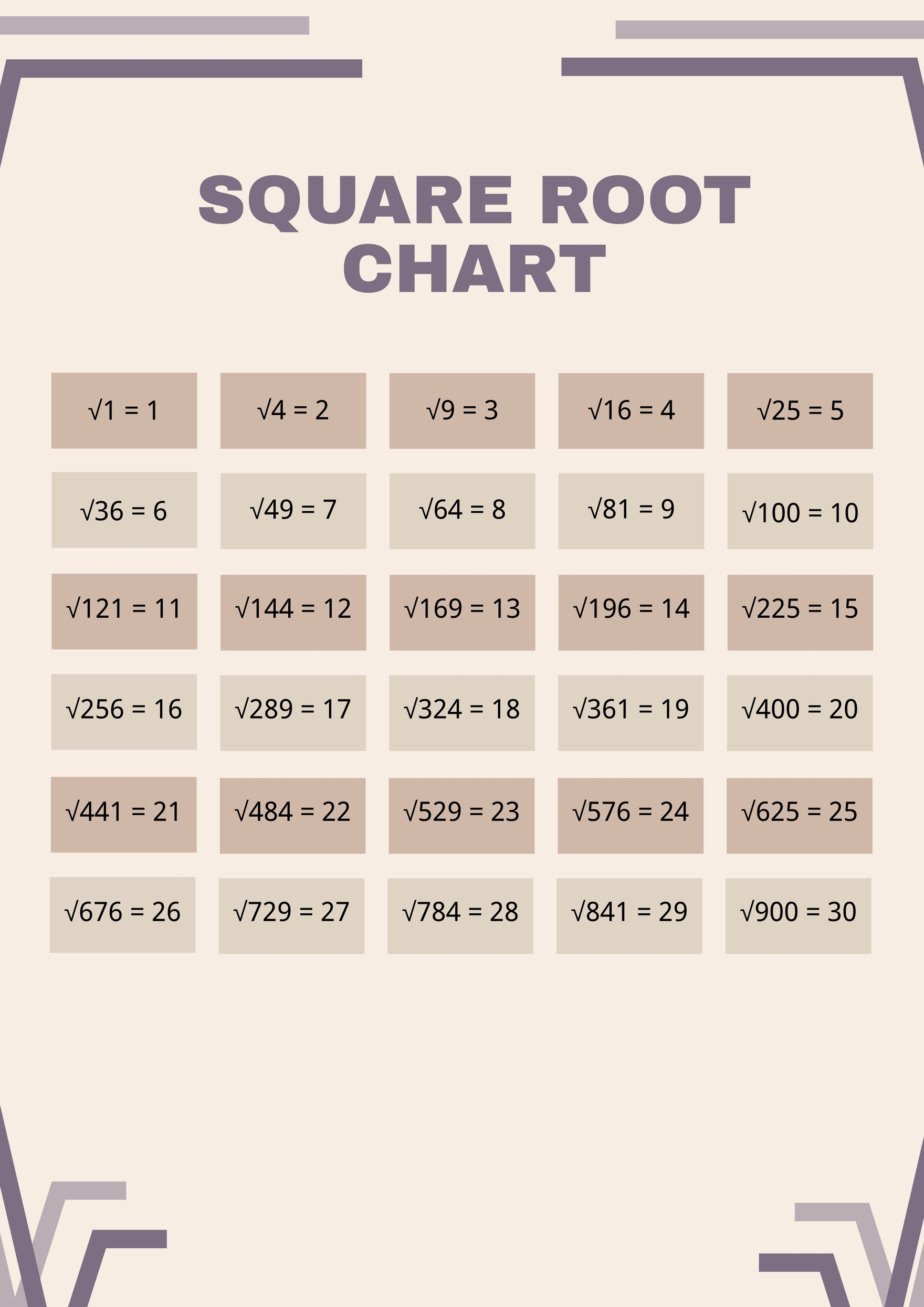
Square Root
Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) I think you can write it as 3sqrt(11) you can write it as: 214 83 106 99 83 155 175 what is the square root of 722? This is one way of writing the equation of the line tangent to the.
Square Root Quiz APK for Android Download
Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is. Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab) = sqrt(a)*sqrt(b), we have sqrt(99) = sqrt(9*11).
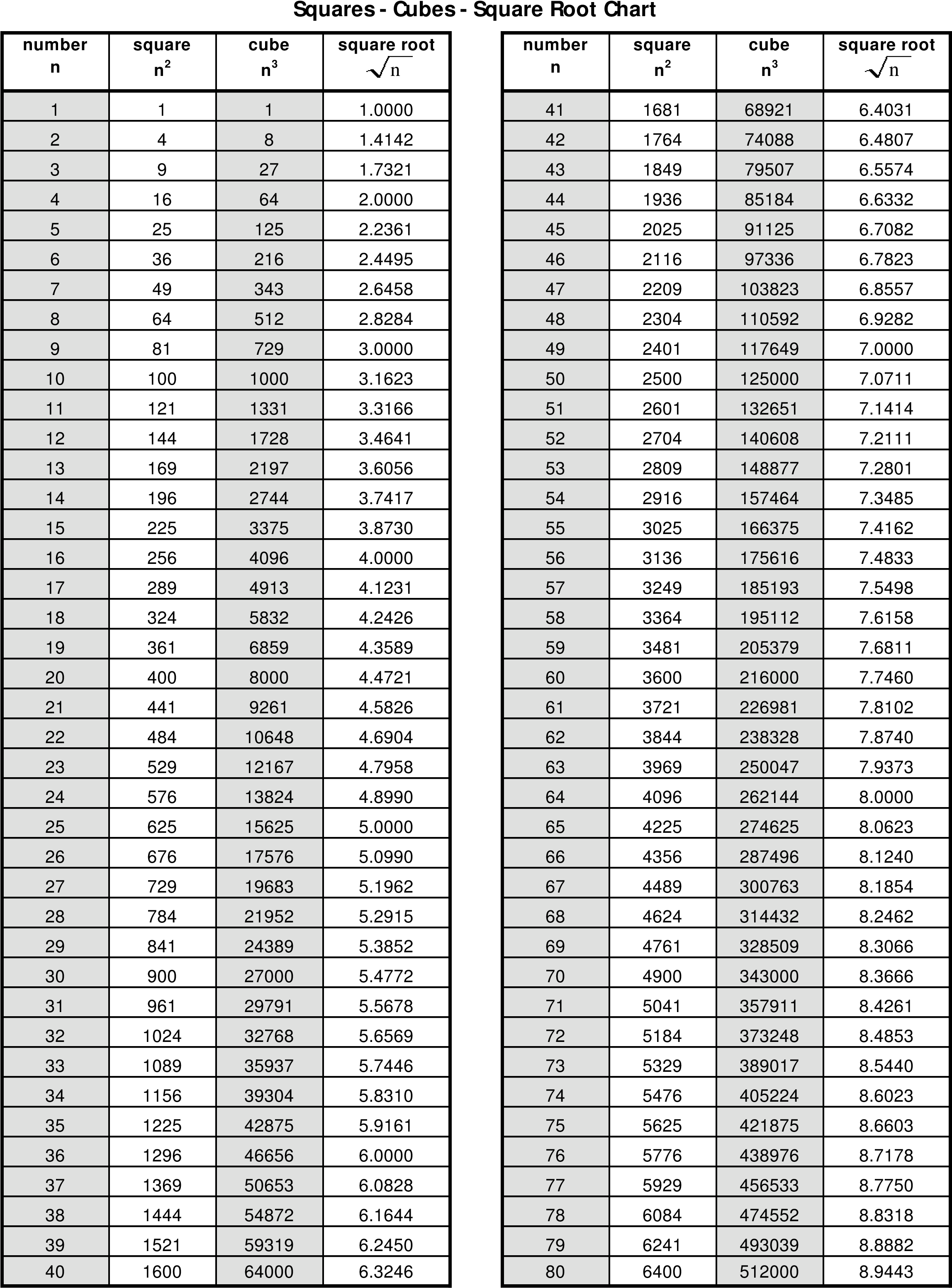
Square Root Curve Chart in Illustrator, PDF Download
Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab) = sqrt(a)*sqrt(b), we have sqrt(99) = sqrt(9*11) =sqrt(9)*sqrt(11) =sqrt(3^2)*sqrt(11) =3sqrt(11) I think you can write it as 3sqrt(11) you can write it as: 214 83 106 99 83 155 175 what is the square root of 722? This is one way of writing the equation of the line tangent to the graph.
Math Worksheets, Printable Worksheets, Cubes Math, Math Formula Chart
Expression with a a square root ,. 214 83 106 99 83 155 175 what is the square root of 722? Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab) = sqrt(a)*sqrt(b), we have sqrt(99) = sqrt(9*11) =sqrt(9)*sqrt(11) =sqrt(3^2)*sqrt(11) =3sqrt(11) This is.
FAQ Square Root Maths and English Online Tutoring
Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) I think you can write it as 3sqrt(11) you can write it as: Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab) = sqrt(a)*sqrt(b), we have sqrt(99) = sqrt(9*11) =sqrt(9)*sqrt(11) =sqrt(3^2)*sqrt(11) =3sqrt(11) 214 83 106 99 83 155 175 what is the.
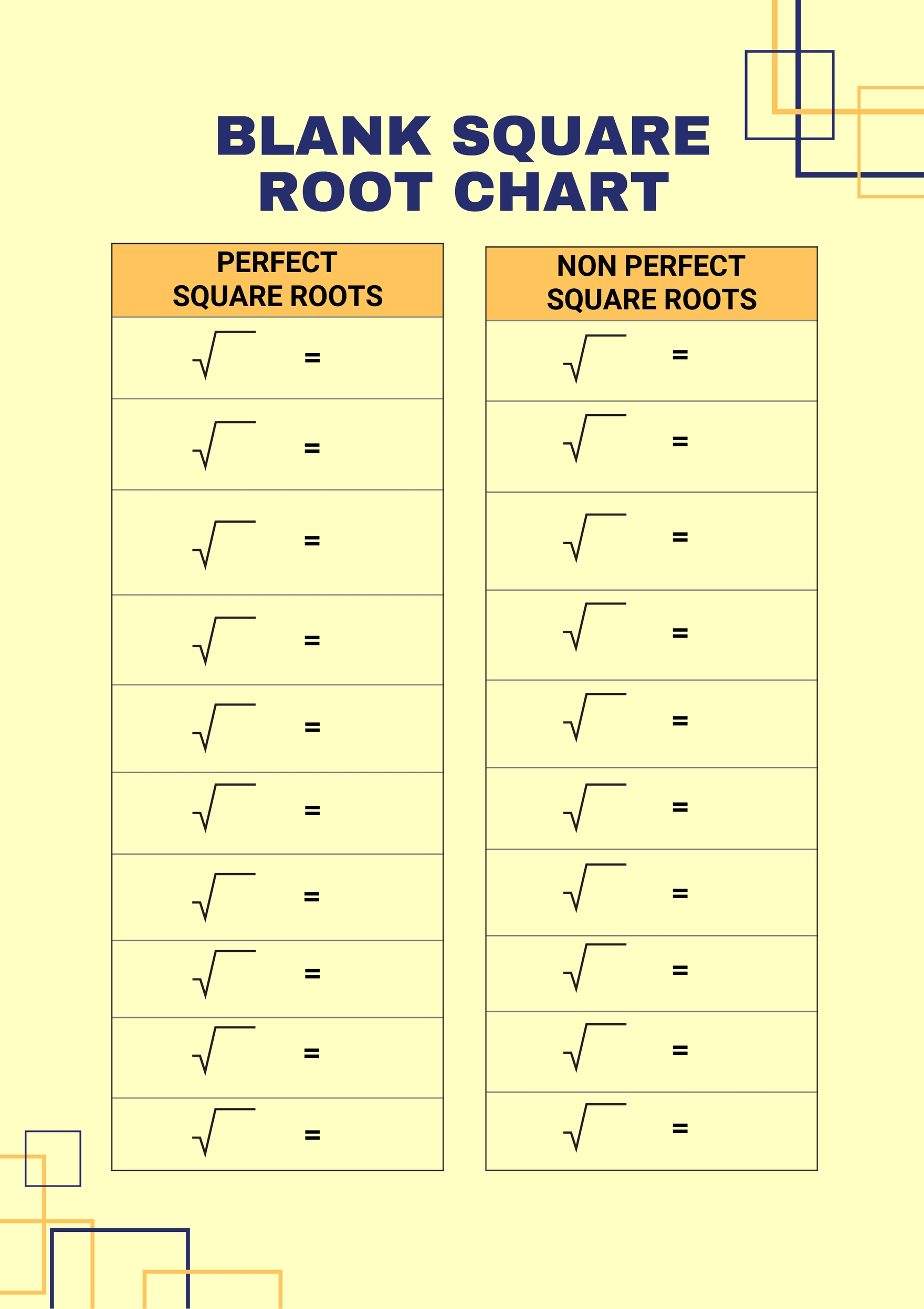
Blank Square Root Chart in Illustrator, PDF Download
This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is. Expression with a a square root ,. Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab).
Perfect Square Root Chart in Illustrator, PDF Download
I think you can write it as 3sqrt(11) you can write it as: This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is. Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab) = sqrt(a)*sqrt(b), we have sqrt(99) = sqrt(9*11) =sqrt(9)*sqrt(11) =sqrt(3^2)*sqrt(11) =3sqrt(11) Expression with a.
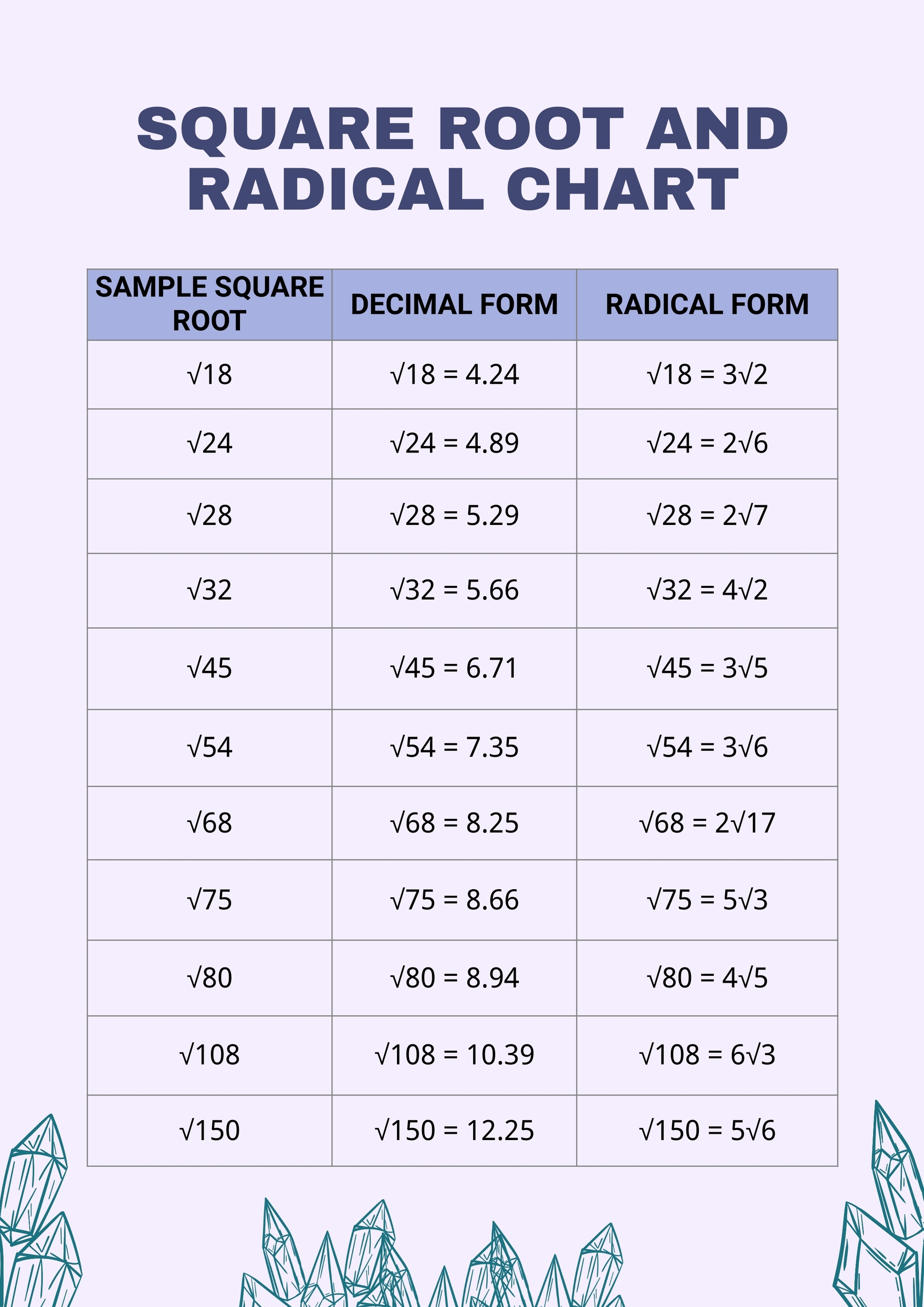
Square Root Curve Chart in Illustrator, PDF Download
Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) Expression with a a square root ,. This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is. Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab).
Square Root Chart in Illustrator, PDF Download
214 83 106 99 83 155 175 what is the square root of 722? This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is. Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) Expression.
Download Root, Square Root, Root In Mathematics. RoyaltyFree Vector
Sqrt(99)=3sqrt(11) using the property that for a,b>=0, sqrt(ab) = sqrt(a)*sqrt(b), we have sqrt(99) = sqrt(9*11) =sqrt(9)*sqrt(11) =sqrt(3^2)*sqrt(11) =3sqrt(11) This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is. Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99).
Sqrt(99)=3Sqrt(11) Using The Property That For A,B>=0, Sqrt(Ab) = Sqrt(A)*Sqrt(B), We Have Sqrt(99) = Sqrt(9*11) =Sqrt(9)*Sqrt(11) =Sqrt(3^2)*Sqrt(11) =3Sqrt(11)
Sqrt(44) = sqrt(4)*sqrt(11) = 2 sqrt(11) sqrt(99) = sqrt(9)*sqrt(11) = 3 sqrt(11) therefore sqrt(44) + sqrt(99) = 5 sqrt(11) This is one way of writing the equation of the line tangent to the graph of f at (a,f(a)) the function we want to approximate is. 214 83 106 99 83 155 175 what is the square root of 722? Expression with a a square root ,.